Graphe¶

Le module matplotlib permet d’afficher des graphes. Le module numpy permet de faire du calcul numérique avec des matrices.

Pour utiliser ces modules, nous devons les importer. Il est tradition de les importer sous les noms raccourcis suivants.

plt pour pyplot
np pour numpy

import matplotlib.pyplot as plt
import numpy as np

Créer un graphe¶

Copiez ce code dans un éditeur de Python et exécutez-le.

import matplotlib.pyplot as plt
import numpy as np

y = [2, 4, 3, 6, 3]

plt.plot(y)
plt.show()

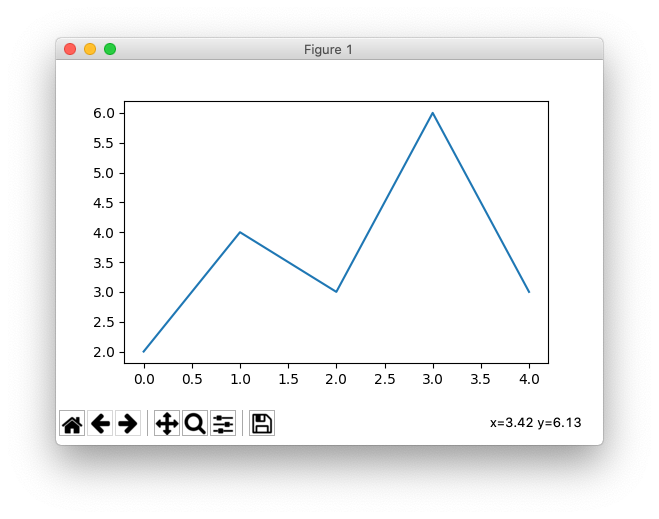
Une fenêtre avec le titre Figure 1 s’ouvre. En bas se trouvent 7 boutons pour zoomer, sauvegarder, etc.

Graphe dans Jupyter¶

Créons une liste de données que nous pouvons afficher. Ici nous créons un tableau numpy. L’avantage est que nous pouvons y additionner facilement un nombre pour le décaler.

y = np.array([2, 4, 3, 6, 3])

Un graphique simple, plot en anglais, est obtenu avec cette commande.

plt.plot(y)

[<matplotlib.lines.Line2D at 0x7fea8f2aaf10>]

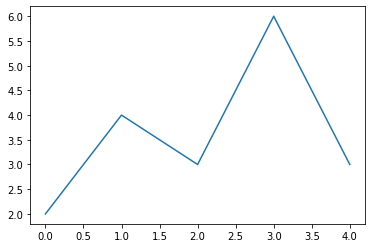
L’objet retourné est de type Line2D qui désigne la courbe. Dorénavant, nous terminons la dernière ligne avec un point-virgule ; pour supprimer cette information.

Attention:
Pour afficher un graphique dans votre éditeur Python standard, vous devez ajouter la commande plt.show() pour l’afficher dans une fenêtre à part.

Titre et légende¶

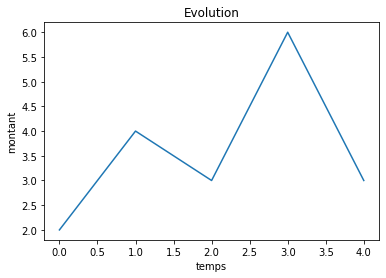
Nous pouvons ajouter un titre ainsi que des légendes pour les deux axes x et y.

plt.title('Evolution')
plt.xlabel('temps')
plt.ylabel('montant')
plt.plot(y);

Couleur des lignes¶

Nous pouvons également ajouter une chaîne de formatage. Les couleurs sont indiquées par les lettres:

r rouge
g vert (green)
b bleu
y jaune (yellow)
m magenta
c cyan
k noir (black)
w blanc (white)

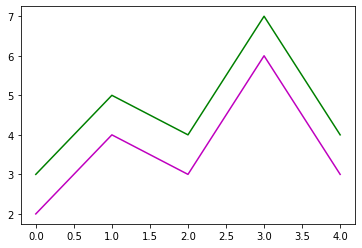
plt.plot(y, 'm', y+1, 'g');

Style des marqueurs¶

La forme des points est indiquée par:

o cercle
s carré (square)
^ triangle (haut)
v triangle (bas)
* astérisque
x x
+ plus

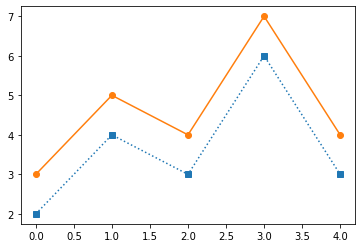
plt.plot(y, 's-', y+1, 'o-');

Format de ligne¶

Le format de ligne est indiqué par:

- solide
: pointillé
-- traitillé
-. mixte

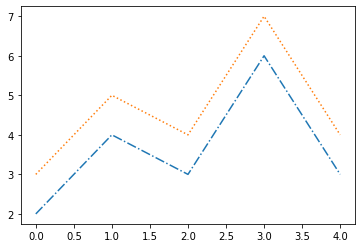
plt.plot(y, '-.', y+1, ':');

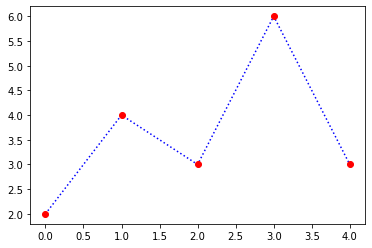
Nous pouvons mélanger deux styles. Pour ceci nous devons afficher deux lignes.

plt.plot(y, 'b:', y, 'or');

Coordonnées en x¶

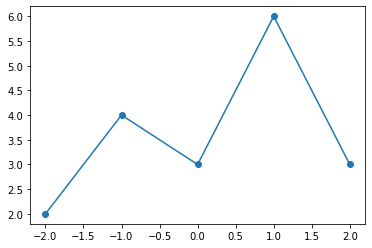
Si nous affichons un graphe à partir d’un seul vecteur, les valeurs x sont des entiers commençants à 0. Nous pouvons définir notre propre plage x, par exemple avec un vecteur x allant de -2 à +2.

x = [-2, -1, 0, 1, 2]
plt.plot(x, y, 'o-');

Propriétés de ligne¶

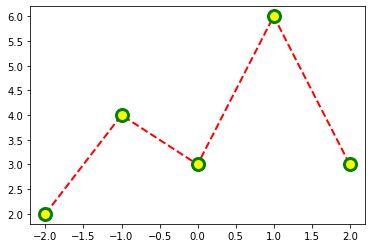
Avec des arguments à option, nous pouvons changer les propriétés d’une ligne.

plt.plot(x, y, color='red', 
         linewidth=2, linestyle='--', 
         marker='o', markersize=12, 
         markerfacecolor='yellow', 
         markeredgewidth=3, markeredgecolor='green');

Légende¶

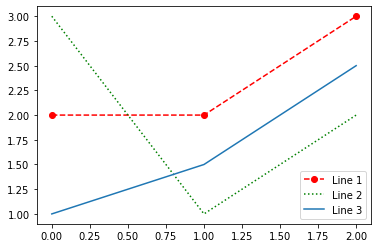
Si nous ajoutons une étiquette aux courbes, nous pouvons afficher une légende avec la fonction legend.

plt.plot([2, 2, 3], 'or--', label='Line 1')
plt.plot([3, 1, 2], 'g:', label='Line 2')
plt.plot([1, 1.5, 2.5], label='Line 3')

plt.legend();

Multiples courbes¶

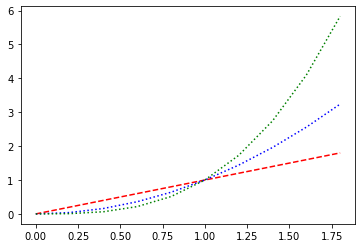
Nous pouvons placer multiples courbes sur un plot.

t = np.arange(0., 2., 0.2)
plt.plot(t, t, 'r--', t, t**2, 'b:', t, t**3, 'g:');

Segments aléatoires¶

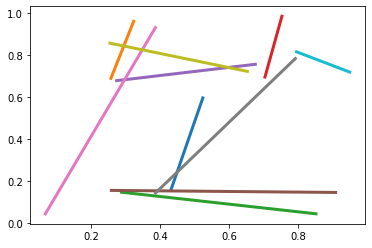
Avec 20 tuples à 2 valeurs, nous pouvons afficher 10 segments aléatories.

plt.plot(*np.random.rand(20, 2), linewidth=3);

Courbes trigonométriques¶

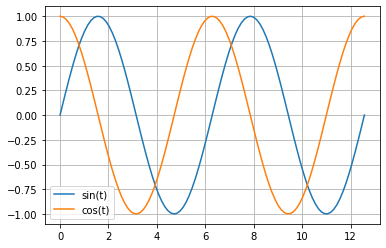
Le module numpy nous permet l’accès facile aux fonctions trigonométriques.

t = np.linspace(0, 4*np.pi, 100)
plt.plot(t, np.sin(t), label='sin(t)')
plt.plot(t, np.cos(t), label='cos(t)')
plt.legend()
plt.grid()

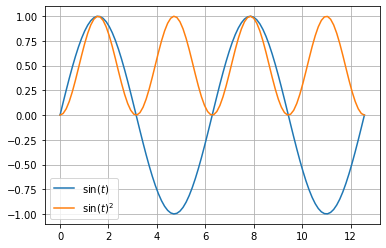
Ici nous affichons le carré du sinus.

\[ f(t) = (\sin t)^2 \]

Les étiquettes peuvent utiliser du LaTeX.

t = np.linspace(0, 4*np.pi, 100)
plt.plot(t, np.sin(t), label='$\sin(t)$')
plt.plot(t, np.sin(t)**2, label='$\sin(t)^2$')
plt.legend()
plt.grid()

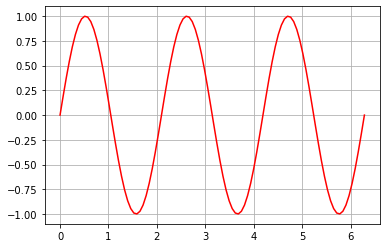
Figures de Lissajous¶

Les figures des Lissajous sont des combinaisons de courbes sinus et cosinus.

t = np.linspace(0, 2*np.pi, 100)
plt.grid()
plt.plot(t, np.sin(3*t), 'r');

plt.grid()
plt.plot(np.sin(t), np.cos(t), 'r');

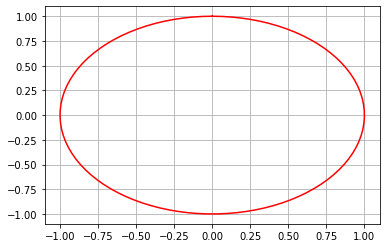
plt.grid()
plt.plot(np.sin(t), np.cos(3*t), 'r');

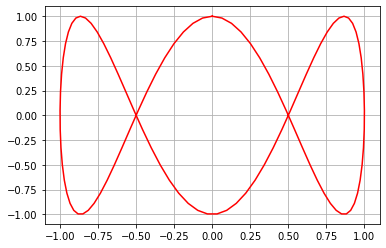
plt.grid()
plt.plot(np.sin(2*t), np.cos(3*t), 'r');

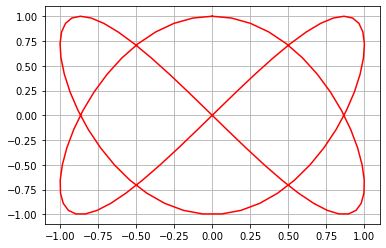
Échelle logarithmique¶

Nous pouvons afficher un des deux axes ou les deux en échelle logarithmique.

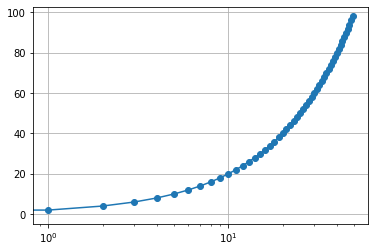
y = np.arange(0, 100, 2)
plt.grid()
plt.plot(y, 'o-')
plt.yscale('log')

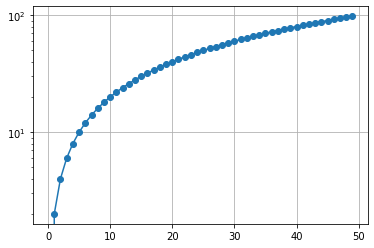
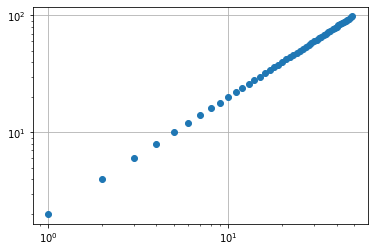
plt.grid()
plt.plot(y, 'o-')
plt.xscale('log')

plt.grid()
plt.plot(y, 'o')
plt.xscale('log')
plt.yscale('log')

La grille¶

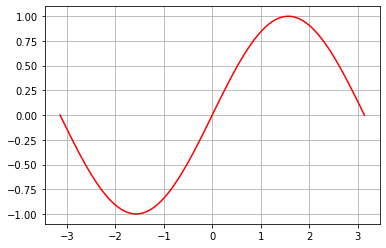
Normalement la grille est alignées avec des entiers.

x = np.linspace(-np.pi, np.pi, 100)
y = np.sin(x)
plt.grid()
plt.plot(x, y, 'r');

Marques de graduation¶

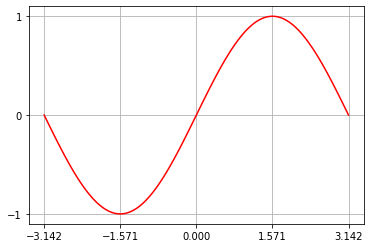
Nous pouvons aligner la grille avec des multiples de \(\pi\).

plt.xticks( [-np.pi, -np.pi/2, 0, np.pi/2, np.pi])
plt.yticks([-1, 0, +1])
plt.grid()
plt.plot(x, y, 'r');

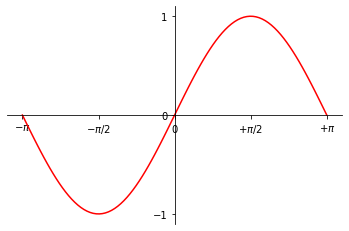
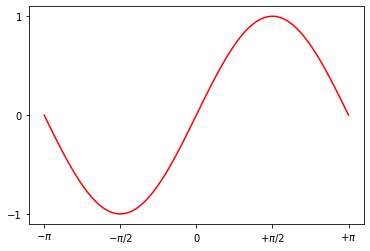
Nous pouvons places des étiquettes en LaTeX.

plt.xticks( [-np.pi, -np.pi/2, 0, np.pi/2, np.pi], 
          ['$-\pi$', '$-\pi/2$', '$0$', '$+\pi/2$', '$+\pi$'])
plt.yticks([-1, 0, +1])
plt.plot(x, y, 'r');

Position des axes¶

En mathématiques, les axes ont leur intersection à l’origine.
Nous supprimons l’axe en haut et à droite et déplaçons les deux autres vers (0, 0).

fig, ax = plt.subplots()
plt.xticks( [-np.pi, -np.pi/2, 0, np.pi/2, np.pi], 
          ['$-\pi$', '$-\pi/2$', '$0$', '$+\pi/2$', '$+\pi$'])
plt.yticks([-1, 0, +1])
plt.plot(x, y, 'r');

ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.spines['bottom'].set_position(('data',0))
ax.spines['left'].set_position(('data',0))

Education numérique