Graphe polaire¶
Les coordonnées polaires sont un système à coordonnées à deux dimensions dans lequel chaque point est déterminé par un angle et une position.
La coordonnée radiale est appelée \(\rho\)
La coordonnée angulaire est appelée \(\theta\)
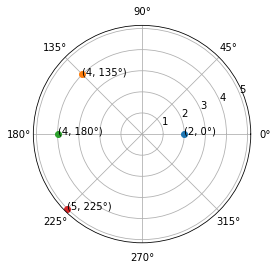
Points¶
Un point (2, 0) est situé à une distance 2 et un angle de 0°.
points = ((2, 0), (4, 135), (4, 180), (5, 225))
for r, theta in points:
t = theta/180*np.pi
plt.polar(t, r, 'o')
plt.text(t, r, f'({r}, {theta}°)')
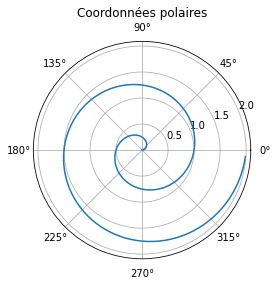
r = np.arange(0, 2, 0.01)
theta = 2 * np.pi * r
plt.polar(theta, r)
plt.gca().set_rticks([0.5, 1, 1.5, 2])
plt.title("Coordonnées polaires");
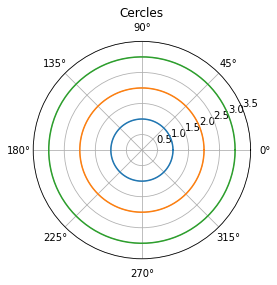
Cercle¶
Un cercle centré sur l’origine est exprimé comme:
\[ r(\theta) = a \]
theta = np.linspace(0, 2*np.pi, 100)
r = np.ones(100)
plt.polar(theta, r)
plt.polar(theta, r*2)
plt.polar(theta, r*3)
plt.ylim(0, 3.5)
plt.title("Cercles");
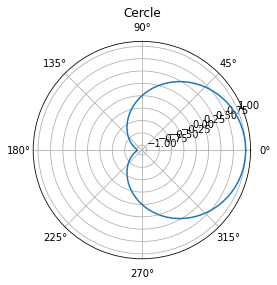
Un cercle passant par l’origine est exprimé comme:
\[ r(\theta) = a \]
theta = np.linspace(0, 2 * np.pi, 100)
plt.polar(theta, np.cos(theta))
plt.title("Cercle");
Rosace¶
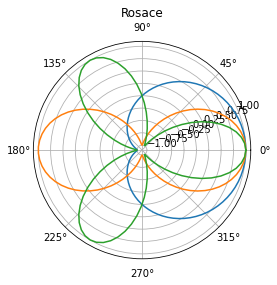
Une rosace est une courbe qui ressemble à des pétales de fleurs. Elle est exprimée par une simple équation polaire.
\[ r(\theta) = a \cos(k \theta + \phi_0) \]
theta = np.linspace(0, 2*np.pi, 100)
plt.polar(theta, np.cos(theta))
plt.polar(theta, np.cos(2 * theta))
plt.polar(theta, np.cos(3 * theta))
plt.title("Rosace");
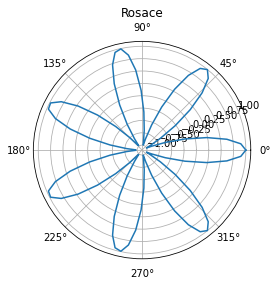
plt.polar(theta, np.cos(7 * theta))
plt.title("Rosace");
Spirale d’Archimède¶
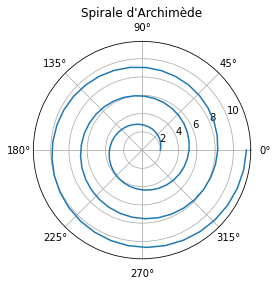
La spirale d’Archimède est une courbe découverte par Archimède. Elle est exprimée par une simple équation polaire.
\[ r(\theta) = a + b \theta \]
theta = np.linspace(0, 6*np.pi, 100)
plt.polar(theta, 2 + 0.5 * theta)
plt.title("Spirale d'Archimède");
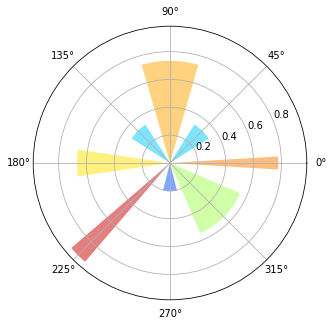
Radar plot¶
ax = plt.axes([0.025, 0.025, 0.95, 0.95], polar=True)
N = 8
theta = np.arange(0.0, 2*np.pi, 2*np.pi/N)
radii = np.random.rand(N)
width = np.pi/4*np.random.rand(N)
bars = plt.bar(theta, radii, width=width, bottom=0.0)
for r, bar in zip(radii, bars):
bar.set_facecolor(plt.cm.jet(r))
bar.set_alpha(0.5)