Algorithmique¶

Un algorithme est une description d’une démarche à suivre par étapes pour faire une tâche précise.

Définition formelle¶

Nous allons mieux définir le concept d’algorithme dans le contexte mathématique ou informatique.

Algorithme simple¶

Un algorithme simple est décrit par

un nom
une entrée
une sortie
des opérations élémentaires

Voici un exemple simple. C’est un algorithme qui incrémente par 2 la valeur d’entrée.

def inc2(a):
    b = a + 2
    return b

Nous y trouvons:

inc2 - un nom
a - une entrée
+ - une opération élémentaire
b - une sortie

Voici un cas concret:

inc2(3)

Algorithme complexe¶

Un algorithme complex contient en plus

des variables
des boucles
des branches conditionnelles
des appels d’autres algorithmes

Voici un exemple d’algorithme qui utilise une boucle. Ici nous calculons la factorielle d’un nombre.

def factoriel(a):
    b = 1
    while a > 0:
        b = b * a
        a = a - 1
    return b

Calculons la factorielle de 3. Le résultat est \(1 \times 2 \times 3 = 6\)

factoriel(3)

Voici maintenant un peu plus compliqué.

factoriel(13)

6227020800

Des listes¶

Nous allons commencer avec des algorithmes qui s’appliquent à des listes.

y = [2, 4, 3, 6, 1]

x = range(len(y))
plt.bar(x, y);

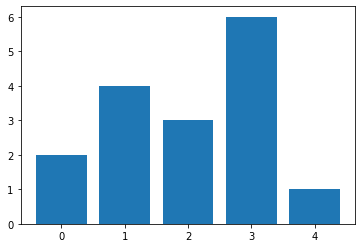
Nous allons utiliser une fonction

Somme¶

Voici un exemple simple pour calculer la somme des éléments d’une liste

l’accumuleur somme est mis à zéro
la liste est parcouru dans une boucle
chaque élément x de la liste est additionné

somme = 0
for x in y:
    somme += x

somme

Nous pouvons définir une

def somme(liste):
    a = 0
    for x in liste:
        a = a + x
    return a

somme(y)

Minimum¶

Pour trouver le minimum nous prenons le premier élément comme minimum actuel. Ensuite nous comparons cette valeur avec tous les autres éléments. Si nous trouvons un plus petit, nous remplaçons le minimum actuel avec celle ci

liste = [4, 2, 3, 6, 1]
m = liste[0]
print('minimum', m)
for x in liste[1:]:
    if x < m:
        m = x
        print('minimum', m)

minimum 4
minimum 2
minimum 1

La fonction suivante visualise le minimum successive.

def minimum(y):
    x = range(len(y))
    plt.bar(x, y)
    
    x0 = [0]
    y0 = [y[0]]
    
    for i, val in enumerate(y):
        if val <= y0[-1]:
            x0.append(i)
            y0.append(val)  
    
    print('min', x0, y0)
    plt.step(x0, y0, 'ro-', linewidth=2, where='post')
    return y[-1]
    
minimum(y)

min [0, 0, 4] [2, 2, 1]

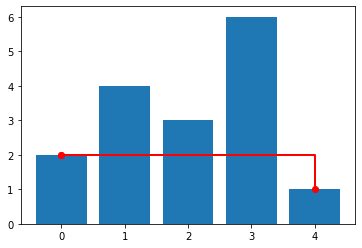
Maximum¶

maximum = liste[0]
for x in liste:
    if x > maximum:
        maximum = x
        
maximum

Enumérer une liste¶

La fonction enumerate() retourne pour chaque élément d’une liste un tuple avec son index et sa valeur (i, val)

a = [3, 5, 4, 6, 2]

for x in enumerate(a):
    print(x)

(0, 3)
(1, 5)
(2, 4)
(3, 6)
(4, 2)

list(enumerate(a))

[(0, 3), (1, 5), (2, 4), (3, 6), (4, 2)]

Position¶

Parfois nous voulons connaitre la position d’un maximum.

a = [3, 5, 4, 6, 2]

max_pos = 0
max_val = a[0]

for i, x in enumerate(a):
    if x > max_val:
        max_pos = i
        max_val = x
        
print(max_val, 'at', max_pos)

6 at 3

for i in range(len(a)):
    if i == 0:
        val, pos = a[0], 0
    elif a[i] > val:
        val, pos = a[i], i
        
print('maximum value', val, 'at position', pos)

maximum value 6 at position 3

Tri par insertion¶

a = [2, 4, 9]

Trouver la position¶

Voici un algorithme pour trouver la position d’une valeur x dans une liste adéjà triée.

def position(a, x):
    for i in range(len(a)):
        if x < a[i]:
            return i
    return i + 1

Nous allons tester l’algorithme avec une liste trié simple, consistant de 2 éléments.

a = [2, 5]
print(position(a, 1))
print(position(a, 3))
print(position(a, 9))

0
1
2

Trouver le minimum¶

Voici un algorithme pour trouver la position du minimum.

def minimum(a):
    pos, val = 0, a[0]
    for i in range(len(a)):
        if a[i] < val:
             pos, val = i, a[i]
    return pos

a = [3, 5, 2, 1, 8]
minimum(a)

Tri par sélection¶

Dans cet algorithme nous cherchons le plus petit élément de la liste et nous l’ajoutons à une nouvelle liste.

a = [5, 6, 9, 7, 3]
b = []
while len(a) > 0:
    i = minimum(a)
    x = a.pop(i)
    b.append(x)
    print(a, '-->', x, '-->', b)

[5, 6, 9, 7] --> 3 --> [3]
[6, 9, 7] --> 5 --> [3, 5]
[9, 7] --> 6 --> [3, 5, 6]
[9] --> 7 --> [3, 5, 6, 7]
[] --> 9 --> [3, 5, 6, 7, 9]

a = [2, 3, 4]
x = a.pop(1)
print(a, x)

[2, 4] 3

a = [2, 3, 4]
a.insert(1, 9)
a

[2, 9, 3, 4]

a = list(range(10))
a

[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

Echanger deux éléments¶

Voici une fonction pour échanger deux éléments d’une liste.

a[3], a[8] = a[8], a[3] 
a

[0, 1, 2, 8, 4, 5, 6, 7, 3, 9]

def swap(a, i, j):
    a[i], a[j] = a[j], a[i] 

swap(a, 1, 2)
a

[0, 2, 1, 8, 4, 5, 6, 7, 3, 9]

Education numérique